売上最適化やリスク評価も!変化を数式で捉える微分積分学の実用性

高校や大学での数学の授業で習得される微分積分学は、一見、抽象的に感じるかもしれませんが、非常に大きな実用的価値を持っています。
微分積分学とは、関数の変化や形状を数学的に捉え、理解する微分と、関数で定義される領域の面積・体積を求める積分からなる学問です。以前の記事でも触れましたが、微分積分学と線形代数学は現代の多くの技術や産業を支えています。この記事では、微分積分学の基本的な考え方と、それが日常生活やビジネスにどのように役立つのかを解説します。
あなたの持つ微分・積分へのイメージは?
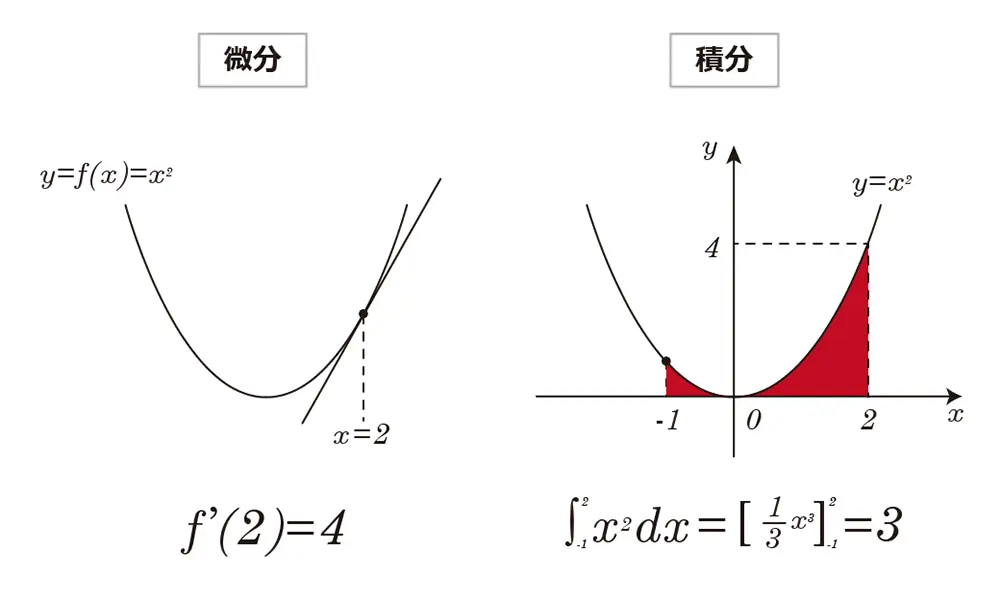
多くの人が、微分積分学を難解な数学として認識しているかもしれません。または、下の図のような計算問題として認識しているでしょうか?しかし、微分積分学は実際には、私たちの周りの多くの現象やビジネスの意思決定に、密接に関わっています。
微分とは変化を捉えること
「微分」とは、変化の割合を表すものです。
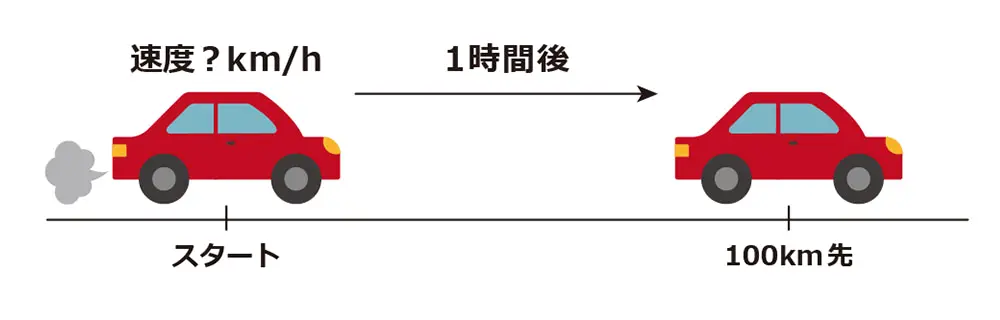
日常生活でよく使われる「速度」を考えてみましょう。車が1時間で100キロメートル進んだら、その速度は100km/1h=100km/hとなります。この「速度」は、移動した距離の変化の割合を示しており、これが微分の基本的な考え方です。
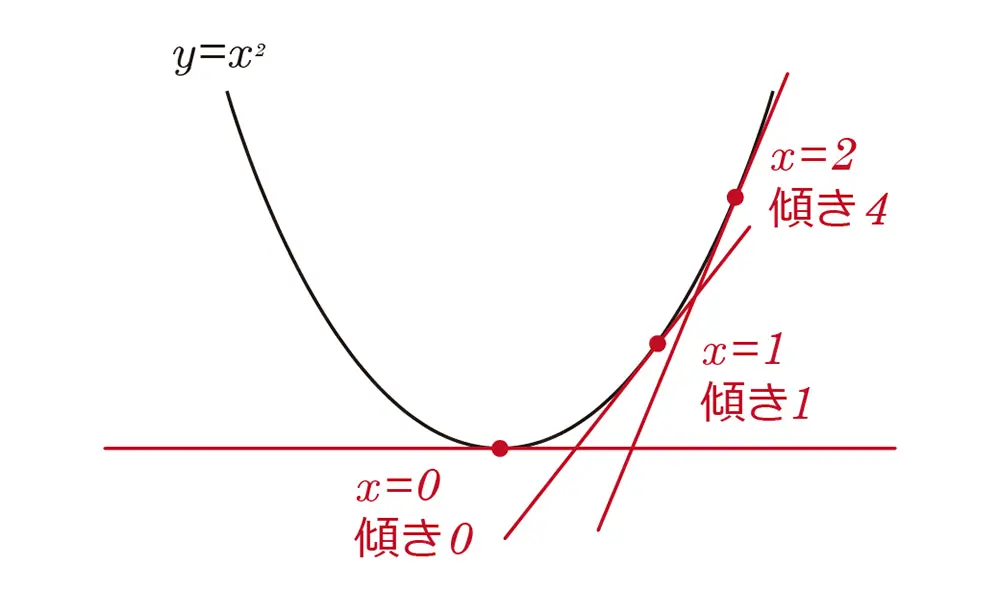
数学的には、グラフがどれだけ傾いているかを知るために微分を使います。例えば、$y = x^2$ という放物線のグラフを考えると、$x=0$の時、グラフは最も平らですが、$x$が増減するにつれて急勾配になります。微分を使うと、その傾きの具体的な度合いを数値で示すことができます。
要するに、微分は「ある瞬間の変化の割合」を知るためのツールです。これにより、物事の変化の様子や傾向を理解し、予測するのに役立てることができます。
最適化に微分が必須
企業が利益を最大化したり、製品の性能を最適化するためには、最適な条件を見つけ出す必要があります。そのための数学的なアプローチとして、微分が不可欠です。
最適化は、多くのビジネスや科学の問題において中心的な役割を果たします。具体的には、ある条件のもとでの最大値や最小値を求めることを指します。例えば、製品のコストを最小にしながら品質を最大にする、あるいは広告予算を最適に配分してリターンを最大化するなど、さまざまなシチュエーションでの「最適」を追求することが求められます。
この「最適」を数学的に探るツールとして微分が登場します。具体的には、ある関数のグラフが最大値や最小値を取る点を見つけるために、微分を使います。微分によって得られる導関数は、グラフの傾きを示すものです。この導関数が0となる点は、元の関数の最大値や最小値となる可能性が高いため、これを利用して最適解を導き出します。
例として、商品の販売価格とその売上高の関係を表すグラフを考えます。価格を高く設定すれば商品1つ当たりの売上は増えますが、高価すぎると購入者の数が減少してしまいます。逆に、価格を低くすれば多くの人が購入するかもしれませんが、商品1つ当たりの売上は少なくなります。適切な価格点を見つけることができれば最大の利益を得ることができるかもしれません。このような最適な価格点を見つけるために、微分を利用してグラフの最大値を探求するのです。また、AIの研究においても学習の過程で最適なモデルのパラメータを見つけるために、微分を使って最適化されています。

モデル化に欠かせない微分方程式
微分方程式とは、前述の導関数を含む方程式であり、さまざまな現象やシステムを数学的に表現するための強力なツールです。特に、時間の経過に伴う変化や、様々な変数間の関係性を捉えるために、この方程式は不可欠です。物理学や化学、生物学、工学など、多岐にわたる分野で微分方程式は活用されています。物理的な現象の理解、化学反応の速度や均衡、生物の成長率や伝染病の拡散モデル、そして電気回路の動作や機械の動き、熱の伝播など、多様な技術や現象に微分方程式の手法が見られます。これにより、複雑な問題を数学的に捉え、精確な解析や予測を行うことが可能となります。
要するに、微分方程式は現実世界の多くの現象を理解し、制御するための鍵となる数学的手法です。

積分とは面積・体積を求めること
積分とは面積・体積を求める数学的な操作で、ある範囲にわたる量を合計するためのものです。簡単に言うと、小さな部分の量を足し合わせて全体の量を知る方法です。
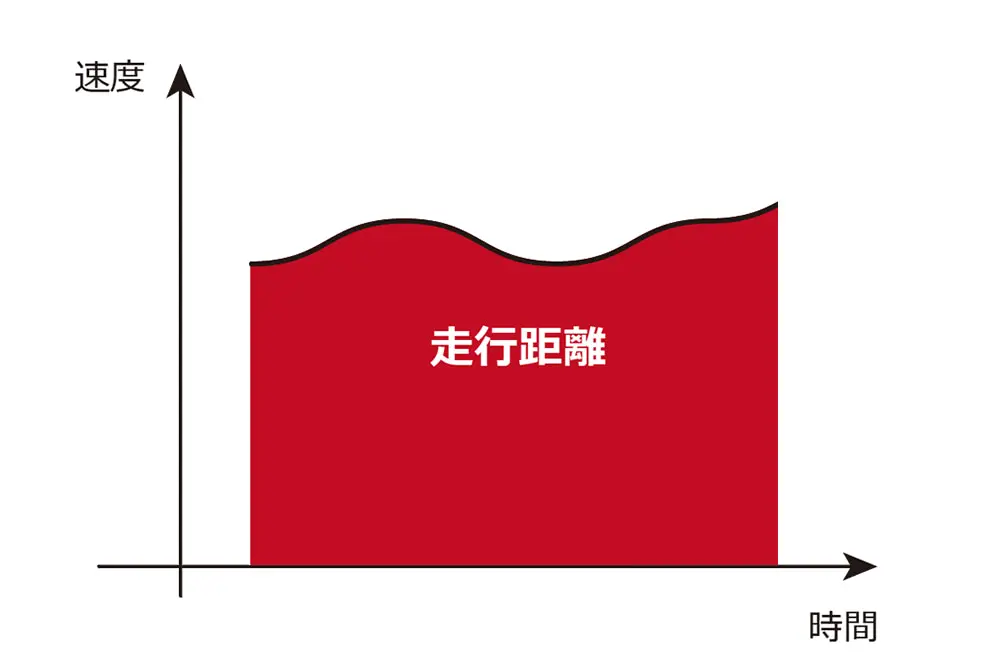
例えば、速度のグラフが与えられたとき、そのグラフの下の面積を計算することで車の走行距離を知ることができます。また、一定期間における商品の売上推移のグラフから、その期間全体の売上の合計を計算するのも積分の応用の一つです。
このように、積分は私たちの日常生活やビジネスの現場でもさまざまな場面で使われています。
積分の多岐にわたる応用
積分は単なる数学の操作に留まらず、実際の科学や工学の多岐にわたる分野で応用されています。物理学において、運動の法則や電磁気学、流体力学などの基本的な法則や方程式の記述には、積分が必要不可欠です。
また、確率論や統計学においても、積分は中心的な役割を果たしています。連続確率変数の確率や期待値、分散の計算は、積分を基にしています。これにより、リスクの評価やデータの解析が可能となります。さらに、工学の分野では、信号処理やフィルタ設計などのアプリケーションにおいても積分の技術が駆使されます。
これらの応用例を通じて、積分がいかに実際の問題解決に貢献しているかがわかります。
微分積分学は現実の問題解決の強力なツール
今回の記事では、線形代数学とともに現代社会のテクノロジーを支える微分積分学について解説しました。
微分は、車の速度、商品の最適な価格設定、さらにAI技術の進化など、私たちの日常の多くの現象や意思決定と深く関わり合っていて、物事の変化の様子や傾向を把握し、それを予測するのに大いに役立っています。
一方、積分は、特定の期間や範囲における量や影響を評価する際のツールとして、多岐にわたって応用されています。統計学でのデータ分布の確率密度関数の面積や期待値の計算、物理学でのエネルギーや物体の移動距離の算出などに使われています。
結論として、微分積分学は、単に抽象的な数学の一部としての位置づけを超え、現実の問題解決の強力なツールとしての役割を果たしています。この分野の深い理解とその適切な利用は、さまざまな分野での成功を実現するための鍵となるでしょう。
参考文献
数学ガールの秘密ノート/積分を見つめて | 結城 浩 | 数学 | Kindleストア | Amazon
スッキリわかる微分積分演習:誤答例・評価基準つき | 皆本 晃弥 | 数学 | Kindleストア | Amazon









