理論やモデル名で知られる研究者たちに学ぶネットワークの科学構造1

ひと言で「ネットワーク」と言っても、研究者の視点で見るとさまざまな理論やモデルがあります。専門的な内容ですが、ネットワーク科学の発展に寄与した研究者たちによって作られた重要な概念に触れながら、代表的なネットワークモデルを紹介します。

グラフ理論の発展に貢献した研究者

初めに、ネットワーク科学の基礎となる「グラフ理論」の発展に貢献した研究者を紹介します。

レオンハルト・オイラー（1707-1783）

18世紀のスイスの数学者であり、グラフ理論の基礎を築き上げた重要な貢献者です。彼の最も有名な業績の一つは、1736年に発表された「ケーニヒスベルクの橋問題」に対する解決法であり、この問題の解決過程でグラフ理論の基本的な概念が生まれました。

「ケーニヒスベルクの橋問題」は、東プロシアの都市ケーニヒスベルクにある川と島を結ぶ7つの橋を、一度だけ通って全ての橋を渡りきることができるかという問題でした。オイラーはこの問題を数学的なアプローチで解決し、その過程で「グラフ」という概念を導入しました。オイラーは問題を数学的にモデル化する際に、橋を点（ノード 頂点）と橋を結ぶ線（エッジ 辺）で表現したグラフを考えました。このようなグラフを用いることで、問題をより抽象的かつ一般的な形に変換することができました。

人やモノのつながる仕組みはコレだ！ネットワークとグラフ理論 送電網やSNSなど、世の中のいろいろなことは、ノードとエッジでつながるネットワークとして説明できます。どうしたら効率的な経路になり、冗長性や距離を適度に維持し、脆弱性を回避できるか？グラフ理論によって計算されています。

彼はさらに、「オイラーグラフ」と呼ばれる特定の性質を持つグラフを定義し、その中で「ケーニヒスベルクの橋問題」を解決しました。オイラーの業績はグラフ理論が独立した数学の分野として確立される礎となり、その後の数学やコンピュータサイエンスの発展に大きな影響を与えました。

フランク・ハラリー（1921-2005）

フランク・ハラリーは、ネットワーク科学とグラフ理論の分野で顕著な貢献をした数学者です。彼の研究は、グラフ理論の基礎を形成し、今日のネットワーク科学に大きな影響を与えています。彼の最も有名な著作は、”Graph Theory”（1969年発行）で、この本はグラフ理論の分野でのスタンダードな教科書として広く認知されています。またこの本では、グラフ理論の基本的な概念や定理やアルゴリズムが紹介され、多くの数学者や科学者に影響を与えました。

ネットワークモデルや理論を発明した研究者1

次に、ネットワークモデルや理論を発明した研究者を紹介します。

ポール・エルデュシュ（1913-1996）

ポール・エルデュシュは20世紀の数学者で、1,500以上もの論文を執筆し、これまでにないほど多くの数学者と共同作業に従事しました。彼が発表した「エルデュシュ数」と呼ばれる指標は、彼との共同論文における協力者の数を示しています。つまり、その数が多いほど、数学者のネットワークにおいて中心的な存在であることの証明です。彼のユニークなアプローチと広範な影響は、数学とネットワークの世界に不可欠なものとなっています。

ネットワーク科学における重要な概念とネットワークモデル

前述した研究者たちは、ネットワークの基礎を確立した人々です。ここからは、ネットワーク科学における重要な概念とネットワークモデルを紹介していきましょう。

無向ネットワーク、有向ネットワーク

以前の記事の復習です。ネットワーク科学を理解する上で重要な要素が2つあり、それが「ノード」と「リンク」です。友人関係のネットワークで考えると、「ノード」が人物で、「リンク」が関係になります。ネットワークには有向と無向が存在し、以下のようにリンクに向きが存在しないネットワークを「無向ネットワーク」と呼びます。

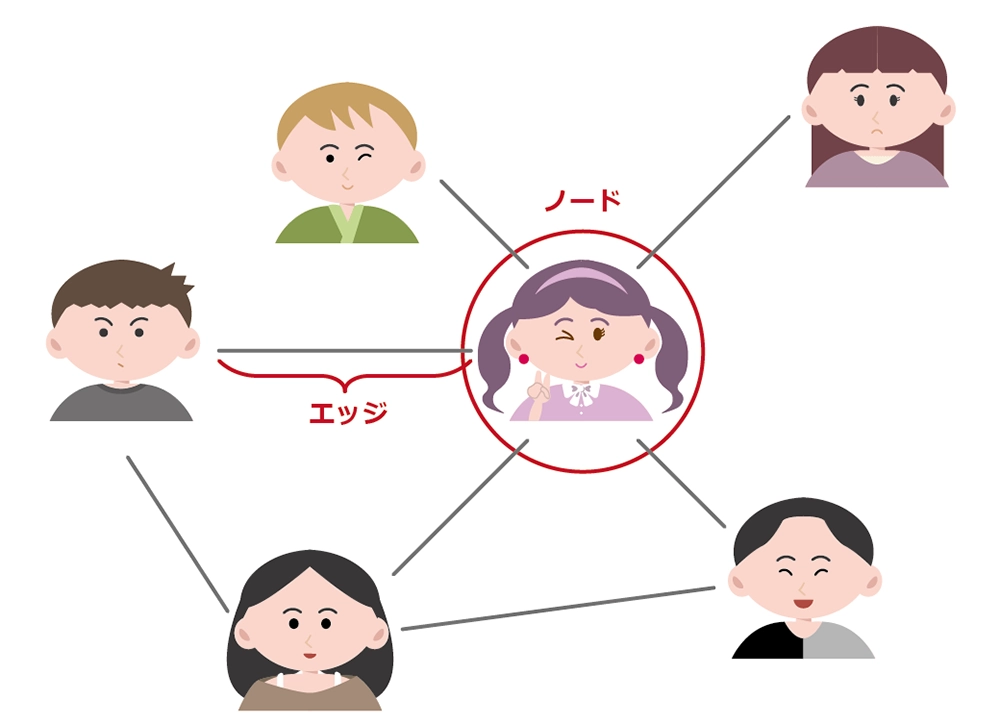
友人同士を結んでいくネットワークの例

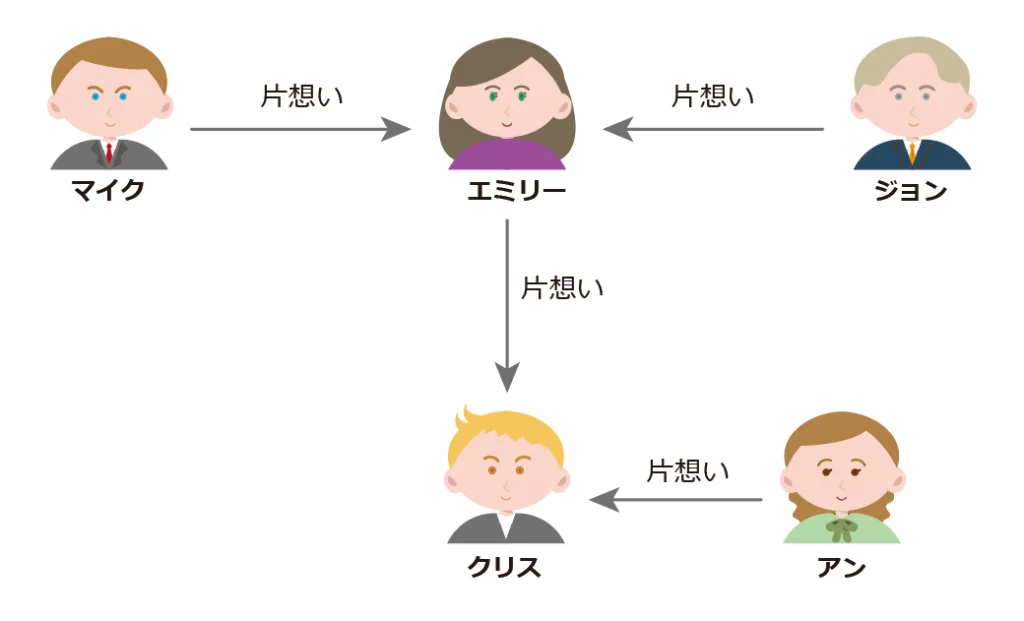
一方以下のネットワークでは、どうでしょうか。以下の図は男女の関係を表すグラフになります。マイクとジョンはエミリーに、エミリーとアンはクリスに思いを寄せている。このように関係性に向きのあるネットワークを、有向ネットワークと呼びます。

代表的なネットワークとネットワークモデル1

次に、代表的なネットワークとネットワークモデルについて紹介します。

ランダムネットワーク

ランダムネットワークは、その名の通りランダムなプロセスに基づいて構築されたネットワークを指します。最もシンプルな形態では、ノードがランダムにエッジで結ばれた 「エルデュシュ・レニーモデル」があります。このモデルは1959年にポール・エルデュシュとアルフレッド・レニィと共に発表しました。このモデルでは、各エッジが一定の確率:pに基づきランダムに選ばれ、ネットワークが形成されます。

<ネットワークを観察してみよう>

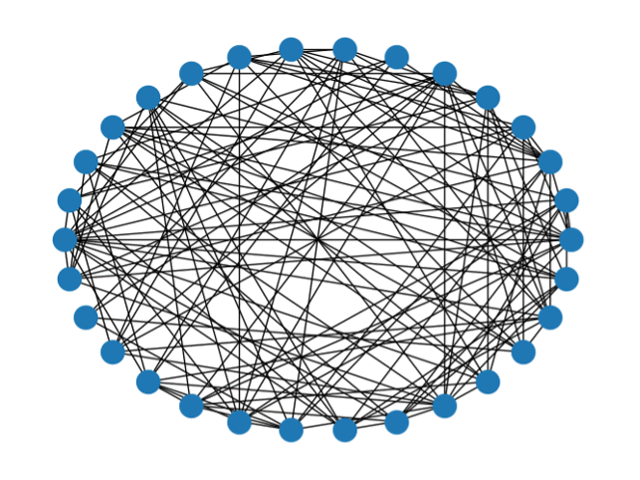
エルデュシュ・レニーモデルを用いて、N（ノードの数）＝30として、確率:pを0.01,0.1,0.3と変化させネットワークを作成しました。p=0.1のネットワークには併せて平均経路長〈d〉と平均クラスター係数〈C〉を併せて示します。確率:pの値が大きくなるにつれて、ネットワークが複雑になっていることが分かります。この確率pは、ネットワークを生成する際にノード間をリンクが結ぶ確率なので、確率が大きくなればなるほど、ノード間がリンクで結ばれるのでネットワークが複雑になります。

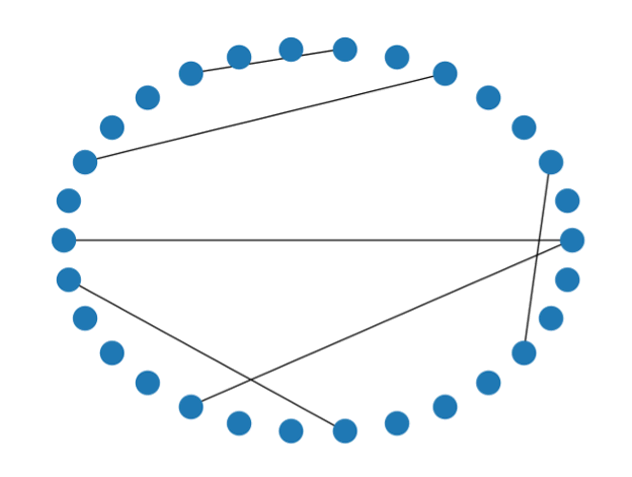
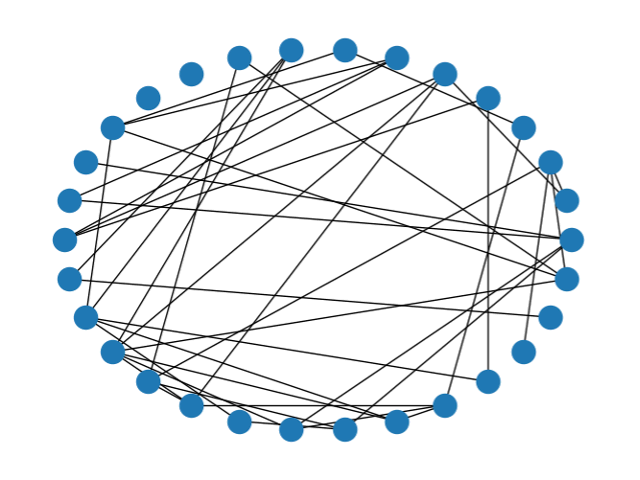
次回は、他の研究者とネットワークモデルについて解説します。

参考

ネットワーク科学 (サイエンス・パレット) | 増田 直紀、高口 太朗、増田 直紀

「複雑ネットワーク」とは何か　複雑な関係を読み解く新しいアプローチ (ブルーバックス) | 増田直紀、今野紀雄

ネットワーク科学: ひと・もの・ことの関係性をデータから解き明かす新しいアプローチ | Albert‐L´aszl´o Barab´asi、池田裕一、井上寛康、谷澤俊弘、京都大学ネットワーク社会研究会

次回は、他の研究者とネットワークモデルについて解説します。 

理論やモデル名で知られる研究者たちに学ぶネットワークの科学構造2 TikTokのインフルエンサーやYouTubeのレコメンド機能も、ネットワーク理論抜きに語れません。高速かつ効果的で柔軟性に富むネットワークの科学構造について、研究者視点で解説します。

福田 慎一郎

ワイン大好き社会人

2021年BlueMemeに新卒で入社。2023年10月からネットワークの統計解析に関する研究開発業務に携わっています。2024年4月から九州大学大学院システム生命科学府に社会人博士学生として入学。科学とアートが好きで、休みの日は美術館や博物館によく行きます。入社してからワインにはまりました。
福田 慎一郎の記事一覧